
Armed with huge amounts of data and computing power to make sense of them, researchers are revisiting some long-held theories about how markets work.
- By
- June 18, 2015
- CBR - Finance

Armed with huge amounts of data and computing power to make sense of them, researchers are revisiting some long-held theories about how markets work.
When TV producers are looking for footage to illustrate financial news, the easiest choice is often the trading floor of an exchange, with traders gesticulating and shouting. This summer, some of those images will be confined to history. CME Group, the world’s biggest futures exchange, is closing almost all the Chicago pits where generations of traders have exchanged futures and options contracts with screams and hand signals. Much of the work of those traders is now automated, executed by algorithms that place thousands of orders every second, and that race each other to reach the exchange’s servers.
This is the latest example of how electronic trading, and more recently high-frequency trading (HFT), has changed the market. But it’s not just the speed and the means of execution that have changed: the data that financial markets produce are changing what we know—or thought we knew—about financial markets. Armed with huge amounts of data, and enough computing power to make sense of them, econometricians and statisticians are revisiting and poking holes in some long-held theories about how markets work. Some of those theories were built on daily data points collected from bound books kept in libraries. But in the high-frequency era, do these hypotheses need to be updated? “There has been a proliferation of data, and that has led to a renaissance in empirical research,” says MIT’s Andrew Lo.
Market practitioners may dismiss some of this work as academic exercise. After all, academics use past data to explain how the market has operated, while practitioners focus on anticipating future market movements. Smart traders use econometric models—many devised by academics, many others by practitioners—as tools “for thinking about things and exploring things, not necessarily as gospel,” says Columbia University’s Emanuel Derman, author of Models. Behaving. Madly.
But Lo compares the relationship between academics and market practitioners to that between scientists and engineers. When academics in finance undertake research, Wall Street engineers take their basic insights and turn them into trading strategies, meaning the research directly shapes automated trading strategies.
Research being conducted by Dacheng Xiu, assistant professor of econometrics and statistics at Chicago Booth, and his collaborators illustrates the change under way. Using snapshots of data, the researchers are poking and prodding at long-held theories, including a methodology that earned its creator a Nobel Prize.
Econometric models tend to be highly geeky. When the University of Chicago’s Lars Peter Hansen won the Nobel Memorial Prize in Economic Sciences in 2013, many journalists struggled to explain his work, the Generalized Method of Moments (GMM). As one of Hansen’s two co-winners, Robert Schiller of Yale, explained in the New York Times, “Professor Hansen has developed a procedure . . . for testing rational-expectations models—models that encompass the efficient-markets model—and his method has led to the statistical rejection of many more of them.” (Eugene F. Fama, Robert R. McCormick Distinguished Service Professor of Finance at Chicago Booth, also shared the Nobel that year.)
Xiu offers another way of thinking about it: the GMM provided a general framework and guidance for how to apply models to real-life data. On Wall Street, he says, traders and their firms use the GMM, or some version of it, to test theoretical models using market data. The GMM functions, therefore, as a bridge between academic theories and empirical data. One industry expert interviewed for this article (using perhaps a narrower definition of GMM than Xiu does) estimates that only half of Wall Street quants know the GMM exists, and only 5 percent of them explicitly use it. Xiu responds that the GMM has been so thoroughly adapted by the financial industry that many traders may not even realize they’re using it.
The GMM was published in 1982, practically ancient history to today’s financial markets. As a tool to link theories to contemporary markets, Xiu says, it has two main limitations. First, today’s markets move far faster than they did in 1982, and a day’s worth of trading volume is many orders of magnitude larger than what it was. Today, many models are built to predict what the market will do in the next hour or minute, rather than the next decade. “Hansen’s approach is designed for long-range time series over decades, and it has to be adapted for this setting,” says Xiu.
Second, though risk has always been a part of trading, the measure of risk—volatility—barely existed 30 years ago. In 1982, Nobel Prize winner Robert Engle of NYU developed the celebrated ARCH model, which described the dynamics of the volatility for the first time. In 1993 the Chicago Board Options Exchange announced real-time reporting of what would become the Volatility Index, commonly known as Wall Street’s “fear gauge.” The VIX, a measurement of the implied volatility of S&P 500 index options, shows how volatile the options market expects the stock market to be in the next 30 days. Since the CBOE in 2003 revised the methodology it uses to calculate the VIX, multiple firms have launched exchange-traded volatility derivatives, and investors have embraced those contracts enthusiastically.
To use the GMM, academics and traders now often have to make strong assumptions, such as assuming that volatility follows a specific pattern or can be perfectly estimated.
Xiu and Duke University’s Jia Li propose a way to tweak the GMM to make it more applicable to contemporary markets. They have created a version that, in homage to the original, they call the Generalized Method of Integrated Moments (GMIM). And they’ve been taking it out for an empirical test-drive using some of the highest-frequency data collected by exchanges and available from data vendors. The CBOE updates VIX data every 15 seconds, while transaction prices of futures and stocks have been time-stamped down to every second. Data updated every millisecond have only recently become available to academics, Xiu says, and he also plans to use them.
Before developing the GMIM, Xiu was part of a team revisiting the late economist Fischer Black’s influential 1976 hypothesis regarding leverage. In the stock market, a stock’s volatility tends to move higher when the stock price moves down—particularly in indexes such as the S&P 500. Black believed that the negative relationship between an asset’s volatility and its return could be explained by a company’s debt-to-equity ratio. When the price of General Motors shares declines, for example, the volatility of the shares rises. Intuitively, it makes sense: the more leveraged a company is, the more volatile its shares are likely to be.
But “to study various financial theories about the leverage effect, one would relate the leverage effect to macroeconomic variables and firm characteristics, which are typically updated at a monthly or quarterly frequency,” write Xiu and the University of Montreal’s Ilze Kalnina. They wanted to evaluate the well-known hypothesis using data from far smaller periods of time.
As their research notes, volatility is estimated rather than precisely measured. A common strategy for overcoming that obstacle has been to create preliminary estimates of volatility over small windows of time, then compute the correlation between those estimates and the investment’s returns. The approach, however, introduces a lot of statistical noise over what econometricians consider short periods, such as a month or a quarter. Even with years of data, the correlation remains insignificant.
Xiu and Kalnina replaced preliminary estimates of volatility with data from two sources: stock prices or index futures, and high-frequency observations available for the VIX or an alternate volatility instrument. Overall, they conclude, there is evidence that Black’s leverage hypothesis still holds: a company’s debt-to-equity ratio helps explain the relationship between volatility and returns. But they also find there could be other factors at work, including credit risk and liquidity risk. The debt-to-equity ratio is “not necessarily the dominant variable,” Xiu says.
Xiu and Kalnina may to some degree be proving what many traders already suspect. Options traders are aware of a pattern called the “volatility smile” that arises in equities indexes such as the S&P 500—implied volatility increases as the strike prices of an option decrease. The leverage hypothesis is one explanation for this pattern, says Derman. He says that traders take the volatility smile into account but don’t necessarily attribute it to the leverage hypothesis.
Questions about the leverage effect led Xiu to question option-pricing models. Of the many things that are modeled in finance, the price of stock options is one of the most fundamental. Options contracts kicked off the financial industry’s quantitative revolution: after the CBOE formed and launched its first contracts, Fischer Black and Myron Scholes devised their famous Black-Scholes model, which traders used to price options. For years, traders and brokers in the trading pits printed out sheets of prices calculated using Black-Scholes.
“Many in the financial industry use Heston and a variety of similar models to value options. Is that wise?”
That model was published long before the VIX index, however, and predated the rise of volatility as an asset class. Black-Scholes assumes that volatility is a constant measurement, while newer models know that volatility actually fluctuates. As a result, many people have replaced Black-Scholes with newer models, the most famous of which is the Heston model, named for the University of Maryland’s Steven L. Heston. An extension of Black-Scholes, Heston assumes that an asset’s volatility is random, not constant, and is correlated with asset returns (the leverage effect mentioned above). Many in the financial industry use Heston and a variety of similar models (the so-called affine models) to value options.
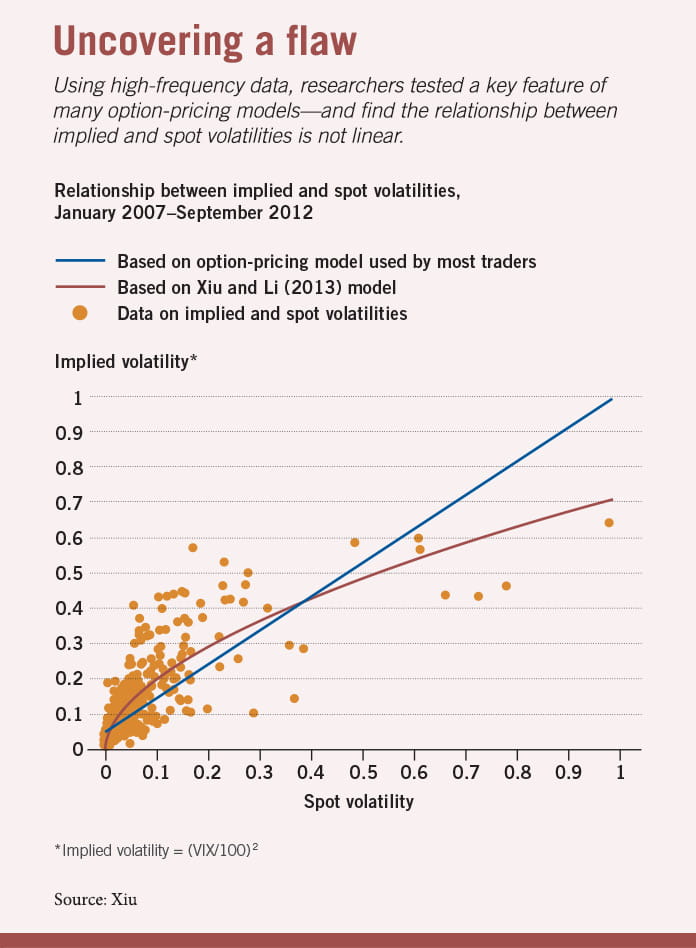
Is that wise? Xiu and Duke’s Jia Li decided to address the question by testing a key feature of these Heston-type models: the linear relationship between spot and implied volatility—spot volatility being the payoff of volatility futures contracts that will expire in the future, and implied volatility being the current market price of the option.
The researchers gathered 23 quarters’ worth of data about implied volatility (using the VIX) and spot volatility (obtained from the S&P 500), spanning 1,457 days. They find that the relationship between spot and implied volatility is actually nonlinear. If you chart the two sets of volatility data, rather than create a consistent line, they veer off from each other, exhibiting what the researchers term “substantial temporal variation.”
Once again, academia may be providing evidence for what practitioners suspect: Heston’s model is flawed. Xiu, who worked at a trading firm before getting his PhD, says many traders have observed that the Heston model doesn’t work. And one industry expert, who asked not to be identified, said that although Heston is popular because it’s in some ways easy to use, it has known weaknesses. But he also said that it would help traders to have the relationship better quantified.
The researchers are also turning the GMIM onto another well-known theoretical model, the Mixture of Distribution Hypothesis (MDH), which dates to the 1970s and predicts a relationship between volatility and liquidity measures such as trading volume. Those are key variables for market-makers’ strategies, and the MDH is one of the models linking them. It holds that good or bad news drives both daily price changes and trading volume.
Northwestern University’s Torben G. Andersen created a modified version in 1996 that produced largely the same results. Andersen did that work well before the explosion in high-frequency data. “A lot of that work I hand-collected,” he says, recalling his library trips to make photocopies of daily stock-price data and trading-volume data. “I don’t know how many books I had to copy these pages from, but it was very tedious work and limited how many stocks you could look at.”
He says that even though volatility has become a bigger feature of the market since that time, volumes have also surged. Institutional investing has grown, trading costs have dropped, and HFT firms have added millions of transactions to global markets every day. Those things have affected volume differently than they have volatility.
Xiu and Li retested the MDH with the GMIM, using four years’ worth of intraday-trading data, aggregated every five minutes. They looked at data from the stock prices of 3M, General Electric, IBM, JP Morgan Chase, and Procter & Gamble.
They find that Andersen’s modified MDH model holds up moderately well. “His model predicts there is a relationship between volume and volatility, and we found supportive evidence of that,” Xiu says. “So when volatility is high, trading volume is as well.”
But the relationship the model predicts between volatility and volume is wrong about half the time. They find, for example, that news has more of an impact during times of crisis. “Our evidence suggests that the modified MDH model needs further refinement in order to fully address the modeling of intraday high-frequency data,” the authors write.
Andersen says that in the 1990s, it was exciting to be able to draw a connection between volatility and volume, but he was aware of the limitations of the data. Xiu and Li, he says, are revisiting the work “in the spirit of how we did it.”
Xiu says the next step for the researchers is to think about how HFT affects the relationship between volatility and liquidity. That requires using higher-frequency data. Xiu and Li have been testing their theories using data collected every second, but Xiu says their method will be able to handle data collected at speeds of less than a second. With trading getting ever faster, even that work will be only scratching the surface of what future statisticians will be able to analyze.—with John Hintze
Your Privacy
We want to demonstrate our commitment to your privacy. Please review Chicago Booth's privacy notice, which provides information explaining how and why we collect particular information when you visit our website.